Zadana je funkcija
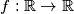
,
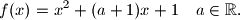

Odredite

tako da bude
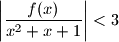
, za svaki
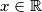
.

Odredite uvjete uz koje je graf funkcije
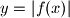
parabola.
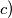
Nađite geometrijsko mjesto tjemena svih parabola
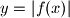
. Nacrtajte sliku!
%V0
Zadana je funkcija $f : \mathbb{R} \rightarrow \mathbb{R}$, $$f(x) = x^2 + (a + 1)x + 1 \quad a \in \mathbb{R} \text{.}$$
$a)$ Odredite $a$ tako da bude $\left| \dfrac{f(x)}{x^2+x+1} \right| < 3$, za svaki $x \in \mathbb{R}$.
$b)$ Odredite uvjete uz koje je graf funkcije $y = |f(x)|$ parabola.
$c)$ Nađite geometrijsko mjesto tjemena svih parabola $y = |f(x)|$. Nacrtajte sliku!