Državno natjecanje 2000 SŠ2 1
Dodao/la:
arhiva1. travnja 2012. Neka je

pozitivan realan broj, a

,
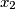
,
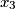
realni brojevi takvi da je
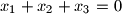
. Dokažite nejednakost
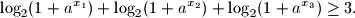
%V0
Neka je $a$ pozitivan realan broj, a $x_1$, $x_2$, $x_3$ realni brojevi takvi da je $x_1 + x_2 + x_3 = 0$. Dokažite nejednakost
$$\log_{2}(1 + a^{x_1}) + \log_{2}(1 + a^{x_2}) + \log_{2}(1 + a^{x_3}) \geq 3.$$
Izvor: Državno natjecanje iz matematike 2000