Državno natjecanje 2000 SŠ2 3
Dodao/la:
arhiva1. travnja 2012. Neka su

i

prirodni brojevi. Dokažite da nejednakost

vrijedi za sve realne brojeve

i

ako i samo ako je

.
(
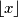
je oznaka za najveći cijeli broj koji nije veći od

.)
%V0
Neka su $j$ i $k$ prirodni brojevi. Dokažite da nejednakost
$$\lfloor (j + k)\alpha \rfloor + \lfloor (j + k)\beta \rfloor \geq \lfloor j\alpha \rfloor + \lfloor j\beta \rfloor + \lfloor k(\alpha + \beta) \rfloor$$
vrijedi za sve realne brojeve $\alpha$ i $\beta$ ako i samo ako je $j = k$.
( $\lfloor x \rfloor$ je oznaka za najveći cijeli broj koji nije veći od $x$.)
Izvor: Državno natjecanje iz matematike 2000