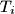
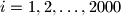
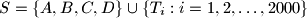
U unutrašnjosti kvadrata stranice duljine , dane su točke , , tako da nikoje tri točke u skupu nisu kolinearne. Dokažite da postoji barem jedan trokut, s vrhovima u skupu , površine manje od .
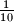
%V0
U unutrašnjosti kvadrata $ABCD$ stranice duljine $20$, dane su točke $T_i$, $i = 1,2,\dots,2000$, tako da nikoje tri točke u skupu $S = \{A,B,C,D\} \cup \{ T_i : i = 1,2,\dots,2000 \}$ nisu kolinearne. Dokažite da postoji barem jedan trokut, s vrhovima u skupu $S$, površine manje od $\frac{1}{10}$.
Školjka 
stranice duljine 
, dane su točke 
, 
, tako da nikoje tri točke u skupu 
nisu kolinearne. Dokažite da postoji barem jedan trokut, s vrhovima u skupu 
, površine manje od 
.