Consider those functions
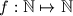
which satisfy the condition
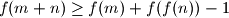
for all
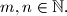
Find all possible values of
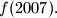
Author: unknown author, Bulgaria
%V0
Consider those functions $f: \mathbb{N} \mapsto \mathbb{N}$ which satisfy the condition
$$f(m + n) \geq f(m) + f(f(n)) - 1$$
for all $m,n \in \mathbb{N}.$ Find all possible values of $f(2007).$
Author: unknown author, Bulgaria