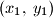
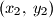
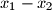
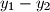
Neka je poligon u koordinatnom sustavu u ravnini čija je površina veća od . Dokažite da postoje dvije različite točke i poligona takve da su i cijeli brojevi.
%V0
Neka je $P$ poligon u koordinatnom sustavu u ravnini čija je površina veća od $1$. Dokažite da postoje dvije različite točke $(x_1,\,y_1)$ i $(x_2,\,y_2)$ poligona $P$ takve da su $x_1 - x_2$ i $y_1 - y_2$ cijeli brojevi.
Školjka 
poligon u koordinatnom sustavu u ravnini čija je površina veća od 
. Dokažite da postoje dvije različite točke 
i 
poligona 
i 
cijeli brojevi.