Državno natjecanje 2003 SŠ2 3
Dodao/la:
arhiva1. travnja 2012. Za pozitivne brojeve

,

,

,

,

označimo
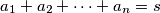
. Dokažite nejednakost
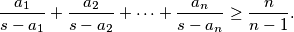
%V0
Za pozitivne brojeve $a_1$, $a_2$, $\dots$, $a_n$, $n \geq 2$ označimo $a_1 + a_2 + \dots + a_n = s$. Dokažite nejednakost
$$\dfrac{a_1}{s - a_1} + \dfrac{a_2}{s - a_2} + \dots + \dfrac{a_n}{s - a_n} \geq \dfrac{n}{n - 1}\text{.}$$
Izvor: Državno natjecanje iz matematike 2003