Državno natjecanje 2008 SŠ2 4
Dodao/la:
arhiva1. travnja 2012. Dan je četverokut

s kutovima
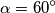
,
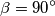
,
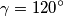
. Dijagonale

i

sijeku se u točki

, pri čemu je
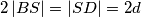
. Iz polovišta

dijagonale

spuštena je okomica
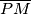
na dijagonalu

, a iz točke

okomica
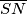
na
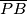
.
Dokaži:
a)
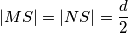
b)
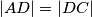
c)
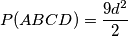
.
%V0
Dan je četverokut $ABCD$ s kutovima $\alpha = {60}^{\circ}$, $\beta = {90}^{\circ}$, $\gamma = {120}^{\circ}$. Dijagonale $\overline{AC}$ i $\overline{BD}$ sijeku se u točki $S$, pri čemu je $2\left\vert BS \right\vert = \left\vert SD \right\vert = 2d$. Iz polovišta $P$ dijagonale $\overline{AC}$ spuštena je okomica $\overline{PM}$ na dijagonalu $\overline{BD}$, a iz točke $S$ okomica $\overline{SN}$ na $\overline{PB}$.
Dokaži:
a) $\displaystyle \left\vert MS \right\vert = \left\vert NS \right\vert = \frac{d}{2}$
b) $\left\vert AD \right\vert = \left\vert DC \right\vert$
c) $\displaystyle P\!\left(ABCD\right) = \frac{9d^2}{2}$.
Izvor: Državno natjecanje iz matematike 2008