Državno natjecanje 2009 SŠ2 2
Dodao/la:
arhiva1. travnja 2012. Dan je četverokut

. Opisana kružnica trokuta

siječe stranice

i
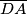
redom u točkama

i

, a opisana kružnica trokuta
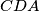
stranice

i

redom u točkama

i

. Pravci
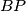
i
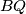
sijeku pravac
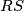
redom u točkama

i

. Dokaži da točke

,

,

i

leže na istoj kružnici.
%V0
Dan je četverokut $ABCD$. Opisana kružnica trokuta $ABC$ siječe stranice $\overline{CD}$ i $\overline{DA}$ redom u točkama $P$ i $Q$, a opisana kružnica trokuta $CDA$ stranice $\overline{AB}$ i $\overline{BC}$ redom u točkama $R$ i $S$. Pravci $BP$ i $BQ$ sijeku pravac $RS$ redom u točkama $M$ i $N$. Dokaži da točke $M$, $N$, $P$ i $Q$ leže na istoj kružnici.
Izvor: Državno natjecanje iz matematike 2009