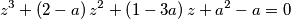
Dokaži da svaki kompleksni broj za koji postoji točno jedan kompleksni broj takav da je zadovoljava jednakost .
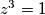
%V0
Dokaži da svaki kompleksni broj $z$ za koji postoji točno jedan kompleksni broj $a$ takav da je $$ z^3 + \left(2-a\right)z^2 + \left(1-3a\right)z + a^2 - a = 0 $$ zadovoljava jednakost $z^3 = 1$.
Školjka 
za koji postoji točno jedan kompleksni broj 
takav da je 
zadovoljava jednakost 
.