Državno natjecanje 2011 SŠ2 2
Dodao/la:
arhiva1. travnja 2012. Neka su

i

realni brojevi takvi da su sve nultočke polinoma
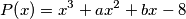
realne. Dokaži da vrijedi
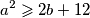
.
%V0
Neka su $a$ i $b$ realni brojevi takvi da su sve nultočke polinoma $$ P\!\left(x\right) = x^3+ax^2+bx-8 $$ realne. Dokaži da vrijedi $\displaystyle a^2 \geqslant 2b + 12$.
Izvor: Državno natjecanje iz matematike 2011