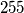
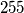
U vreći se nalazilo kuglica označenih brojevima , , ..., , a onda je svaki od učenika uzeo iz vreće po jednu kuglicu. Pokazalo se da nijedan od izvučenih brojeva nije točno dvostruko veći od nekog drugog izvučenog broja. Odredi najveći mogući .
%V0
U vreći se nalazilo $255$ kuglica označenih brojevima $1$, $2$, ..., $255$, a onda je svaki od $N$ učenika uzeo iz vreće po jednu kuglicu. Pokazalo se da nijedan od izvučenih brojeva nije točno dvostruko veći od nekog drugog izvučenog broja. Odredi najveći mogući $N$.
Školjka 
kuglica označenih brojevima 
, 
, ..., 
učenika uzeo iz vreće po jednu kuglicu. Pokazalo se da nijedan od izvučenih brojeva nije točno dvostruko veći od nekog drugog izvučenog broja. Odredi najveći mogući