Let

be an isosceles triangle with
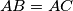
.

is the midpoint of

and
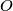
is the point on the line
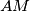
such that
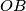
is perpendicular to

.

is an arbitrary point on

different from

and

.

lies on the line

and

lies on the line

such that
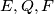
are distinct and collinear. Prove that
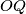
is perpendicular to
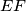
if and only if
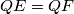
.
%V0
Let $ABC$ be an isosceles triangle with $AB = AC$. $M$ is the midpoint of $BC$ and $O$ is the point on the line $AM$ such that $OB$ is perpendicular to $AB$. $Q$ is an arbitrary point on $BC$ different from $B$ and $C$. $E$ lies on the line $AB$ and $F$ lies on the line $AC$ such that $E, Q, F$ are distinct and collinear. Prove that $OQ$ is perpendicular to $EF$ if and only if $QE = QF$.