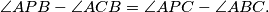
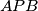
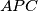
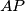
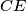
Let be a point inside a triangle such that Let , be the incenters of triangles , , respectively. Show that the lines , , meet at a point.
%V0
Let $P$ be a point inside a triangle $ABC$ such that
$$\angle APB - \angle ACB = \angle APC - \angle ABC.$$
Let $D$, $E$ be the incenters of triangles $APB$, $APC$, respectively. Show that the lines $AP$, $BD$, $CE$ meet at a point.
Izvor: Međunarodna matematička olimpijada, shortlist 1996
Školjka 
be a point inside a triangle 
such that 
, 
be the incenters of triangles 
, 
, respectively. Show that the lines 
, 
, 
meet at a point.