Let
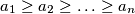
be real numbers such that for all integers
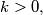
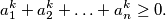
Let
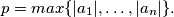
Prove that
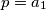
and that
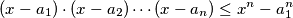
for all
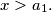
%V0
Let $a_1 \geq a_2 \geq \ldots \geq a_n$ be real numbers such that for all integers $k > 0,$
$$a^k_1 + a^k_2 + \ldots + a^k_n \geq 0.$$
Let $p = max\{|a_1|, \ldots, |a_n|\}.$ Prove that $p = a_1$ and that
$$(x - a_1) \cdot (x - a_2) \cdots (x - a_n) \leq x^n - a^n_1$$ for all $x > a_1.$