Let
be a point inside a triangle
such that
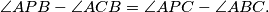
Let
,
be the incenters of triangles
,
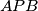
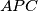
, respectively. Show that the lines
,
,
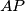
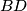
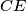
meet at a point.
%V0
Let $P$ be a point inside a triangle $ABC$ such that
$$\angle APB - \angle ACB = \angle APC - \angle ABC.$$
Let $D$, $E$ be the incenters of triangles $APB$, $APC$, respectively. Show that the lines $AP$, $BD$, $CE$ meet at a point.
Školjka