Let

be a point inside a triangle

such that
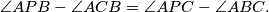
Let

,

be the incenters of triangles
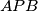
,
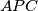
, respectively. Show that the lines
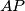
,

,
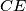
meet at a point.
%V0
Let $P$ be a point inside a triangle $ABC$ such that
$$\angle APB - \angle ACB = \angle APC - \angle ABC.$$
Let $D$, $E$ be the incenters of triangles $APB$, $APC$, respectively. Show that the lines $AP$, $BD$, $CE$ meet at a point.