a) Služeći se poznatim formulama 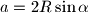 i
i 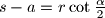 u trokutu
u trokutu  s polumjerima
s polumjerima  i
i  opisane i upisane kružnice i poluopsegom
opisane i upisane kružnice i poluopsegom  i izražavajući
i izražavajući 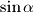 i
i 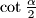 pomoću
pomoću 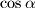 pokažite da je broj
pokažite da je broj 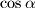 rješenje jednadžbe
rješenje jednadžbe
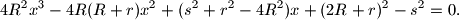
b) Izrazite brojeve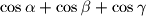 i
i 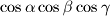 pomoću duljina
pomoću duljina  ,
,  i
i  .
.
c) Pokažite da je zbroj orijentiranih udaljenosti središta opisane kružnice trokuta
opisane kružnice trokuta  od pravaca
od pravaca  ,
,  ,
,  jednaka
jednaka 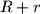 , ako se orijentirana udaljenost točke
, ako se orijentirana udaljenost točke  od npr. pravca
od npr. pravca  uzima kao pozitivna ili negativna već prema tome da li su točke
uzima kao pozitivna ili negativna već prema tome da li su točke  i
i  s iste ili s različitih strana tog pravca.
s iste ili s različitih strana tog pravca.
d) Ako se konveksan tetivni -terokut na bilo koji način podijeli na
-terokut na bilo koji način podijeli na  trokuta pomoću
trokuta pomoću 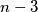 dijagonala, koje se ne sijeku unutar tog poligona, pokažite da je zbroj polumjera upisanih kružnica tih trokuta stalan bez obzira na podjelu na trokute.
dijagonala, koje se ne sijeku unutar tog poligona, pokažite da je zbroj polumjera upisanih kružnica tih trokuta stalan bez obzira na podjelu na trokute.
(Napomena: Ovaj zadatak vrijedi bodova (ostali po
bodova (ostali po 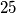 ), a pri rješavanju pojedinog dijela ovog zadatka dopušteno je koristiti ranije dijelove makar i ne bili riješeni.)
), a pri rješavanju pojedinog dijela ovog zadatka dopušteno je koristiti ranije dijelove makar i ne bili riješeni.)
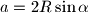 i
i 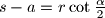 u trokutu
u trokutu  s polumjerima
s polumjerima  i
i  opisane i upisane kružnice i poluopsegom
opisane i upisane kružnice i poluopsegom  i izražavajući
i izražavajući 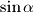 i
i 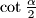 pomoću
pomoću 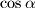 pokažite da je broj
pokažite da je broj 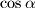 rješenje jednadžbe
rješenje jednadžbe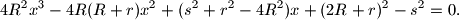
b) Izrazite brojeve
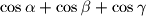 i
i 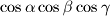 pomoću duljina
pomoću duljina  ,
,  i
i  .
.c) Pokažite da je zbroj orijentiranih udaljenosti središta
 opisane kružnice trokuta
opisane kružnice trokuta  od pravaca
od pravaca  ,
,  ,
,  jednaka
jednaka 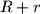 , ako se orijentirana udaljenost točke
, ako se orijentirana udaljenost točke  od npr. pravca
od npr. pravca  uzima kao pozitivna ili negativna već prema tome da li su točke
uzima kao pozitivna ili negativna već prema tome da li su točke  i
i  s iste ili s različitih strana tog pravca.
s iste ili s različitih strana tog pravca.d) Ako se konveksan tetivni
 -terokut na bilo koji način podijeli na
-terokut na bilo koji način podijeli na  trokuta pomoću
trokuta pomoću 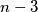 dijagonala, koje se ne sijeku unutar tog poligona, pokažite da je zbroj polumjera upisanih kružnica tih trokuta stalan bez obzira na podjelu na trokute.
dijagonala, koje se ne sijeku unutar tog poligona, pokažite da je zbroj polumjera upisanih kružnica tih trokuta stalan bez obzira na podjelu na trokute.(Napomena: Ovaj zadatak vrijedi
 bodova (ostali po
bodova (ostali po 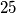 ), a pri rješavanju pojedinog dijela ovog zadatka dopušteno je koristiti ranije dijelove makar i ne bili riješeni.)
), a pri rješavanju pojedinog dijela ovog zadatka dopušteno je koristiti ranije dijelove makar i ne bili riješeni.)  Školjka
Školjka