Slični zadaci
Consider two monotonically decreasing sequences 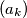 and
and  , where
, where 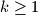 , and
, and 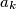 and
and 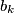 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences
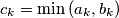 ;
;
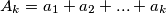 ;
;
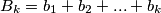 ;
;
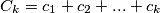
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences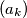 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 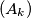 and
and 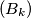 are not bounded, while the sequence
are not bounded, while the sequence 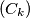 is bounded?
is bounded?
(b) Does the answer to problem (a) change if we stipulate that the sequence must be
must be 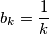 for all k ?
for all k ?
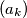 and
and  , where
, where 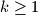 , and
, and 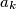 and
and 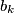 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences 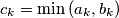 ;
; 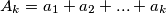 ;
; 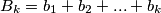 ;
; 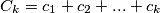
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences
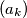 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 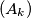 and
and 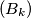 are not bounded, while the sequence
are not bounded, while the sequence 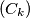 is bounded?
is bounded? (b) Does the answer to problem (a) change if we stipulate that the sequence
 must be
must be 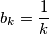 for all k ?
for all k ? Let 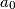 ,
,  ,
, 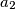 , ... be an infinite sequence of real numbers satisfying the equation
, ... be an infinite sequence of real numbers satisfying the equation 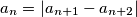 for all
for all 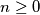 , where
, where 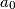 and
and  are two different positive reals.
are two different positive reals.
Can this sequence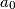 ,
,  ,
, 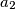 , ... be bounded?
, ... be bounded?
Remark This one is from the IMO Shortlist 2004, but it's already published on the official BWM website und thus I take the freedom to post it here:
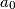 ,
,  ,
, 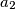 , ... be an infinite sequence of real numbers satisfying the equation
, ... be an infinite sequence of real numbers satisfying the equation 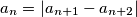 for all
for all 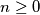 , where
, where 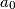 and
and  are two different positive reals.
are two different positive reals. Can this sequence
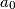 ,
,  ,
, 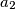 , ... be bounded?
, ... be bounded? Remark This one is from the IMO Shortlist 2004, but it's already published on the official BWM website und thus I take the freedom to post it here:
 Školjka
Školjka 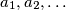 be an infinite sequence of real numbers, for which there exists a real number
be an infinite sequence of real numbers, for which there exists a real number  with
with 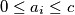 for all
for all  , such that
, such that 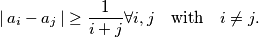
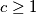 .
. 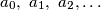 is a sequence of real numbers such that
is a sequence of real numbers such that ![a_{n + 1} = \left[a_{n}\right]\cdot \left\{a_{n}\right\}](/media/m/8/4/1/841a9a2ad06c20187088b2f582b7c6d1.png)
 such that for every
such that for every 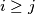 we have
we have 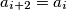 .
. 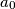 ,
, 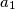 ,
, 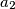 ,
,  be a sequence of reals such that
be a sequence of reals such that 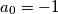 and
and 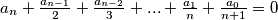 for all
for all 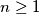 .
. 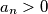 for all
for all  određeni su cijeli brojevi
određeni su cijeli brojevi  i
i 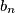 tako da je
tako da je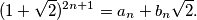
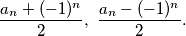
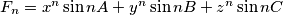 , gdje su
, gdje su 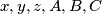 realni brojevi takvi da je
realni brojevi takvi da je 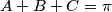 . Ako je
. Ako je 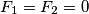 , dokažite da je
, dokažite da je 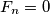 za svaki prirodni broj
za svaki prirodni broj