Find all functions
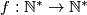
satisfying
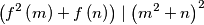
for any two positive integers

and

.
Remark. The abbreviation
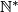
stands for the set of all positive integers:

.
By
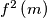
, we mean
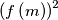
(and not
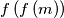
).
%V0
Find all functions $f: \mathbb{N^{*}}\to \mathbb{N^{*}}$ satisfying
$$\left(f^{2}\left(m\right)+f\left(n\right)\right) \mid \left(m^{2}+n\right)^{2}$$
for any two positive integers $m$ and $n$.
Remark. The abbreviation $\mathbb{N^{*}}$ stands for the set of all positive integers:
$\mathbb{N^{*}}=\left\{1,2,3,...\right\}$.
By $f^{2}\left(m\right)$, we mean $\left(f\left(m\right)\right)^{2}$ (and not $f\left(f\left(m\right)\right)$).