Prove that for any four positive real numbers

,

,

,

the inequality
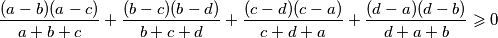
holds. Determine all cases of equality.
Author: Darij Grinberg (Problem Proposal), Christian Reiher (Solution), Germany
%V0
Prove that for any four positive real numbers $a$, $b$, $c$, $d$ the inequality
$$\frac {(a - b)(a - c)}{a + b + c} + \frac {(b - c)(b - d)}{b + c + d} + \frac {(c - d)(c - a)}{c + d + a} + \frac {(d - a)(d - b)}{d + a + b} \geqslant 0$$
holds. Determine all cases of equality.
Author: Darij Grinberg (Problem Proposal), Christian Reiher (Solution), Germany