IMO Shortlist 2006 problem A6
Dodao/la:
arhiva2. travnja 2012. Determine the least real number
such that the inequality
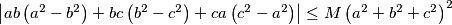
holds for all real numbers
,
and
.
%V0
Determine the least real number $M$ such that the inequality
$\left|ab\left(a^{2}-b^{2}\right)+bc\left(b^{2}-c^{2}\right)+ca\left(c^{2}-a^{2}\right)\right| \leq M\left(a^{2}+b^{2}+c^{2}\right)^2$
holds for all real numbers $a$, $b$ and $c$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006
Školjka 
