In a triangle  , let
, let 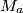 ,
, 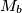 ,
, 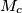 be the midpoints of the sides
be the midpoints of the sides  ,
,  ,
,  , respectively, and
, respectively, and 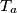 ,
, 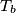 ,
, 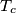 be the midpoints of the arcs
be the midpoints of the arcs  ,
,  ,
,  of the circumcircle of
of the circumcircle of  , not containing the vertices
, not containing the vertices  ,
,  ,
,  , respectively. For
, respectively. For 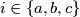 , let
, let 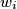 be the circle with
be the circle with 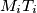 as diameter. Let
as diameter. Let 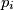 be the common external common tangent to the circles
be the common external common tangent to the circles 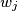 and
and 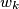 (for all
(for all 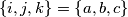 ) such that
) such that 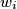 lies on the opposite side of
lies on the opposite side of 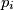 than
than 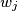 and
and 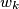 do.
do.
Prove that the lines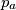 ,
, 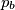 ,
, 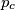 form a triangle similar to
form a triangle similar to  and find the ratio of similitude.
and find the ratio of similitude.
 , let
, let 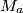 ,
, 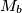 ,
, 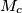 be the midpoints of the sides
be the midpoints of the sides  ,
,  ,
,  , respectively, and
, respectively, and 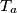 ,
, 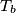 ,
, 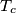 be the midpoints of the arcs
be the midpoints of the arcs  ,
,  ,
,  of the circumcircle of
of the circumcircle of  , not containing the vertices
, not containing the vertices  ,
,  ,
,  , respectively. For
, respectively. For 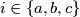 , let
, let 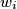 be the circle with
be the circle with 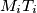 as diameter. Let
as diameter. Let 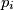 be the common external common tangent to the circles
be the common external common tangent to the circles 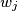 and
and 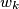 (for all
(for all 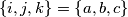 ) such that
) such that 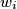 lies on the opposite side of
lies on the opposite side of 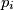 than
than 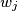 and
and 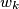 do.
do. Prove that the lines
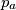 ,
, 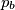 ,
, 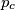 form a triangle similar to
form a triangle similar to  and find the ratio of similitude.
and find the ratio of similitude. Slični zadaci
Let  be an odd prime and
be an odd prime and  a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length
a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length 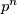 . Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by
. Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by 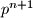 .
.
 be an odd prime and
be an odd prime and  a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length
a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length 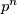 . Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by
. Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by 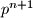 .
. Points 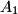 ,
, 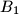 ,
, 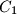 are chosen on the sides
are chosen on the sides  ,
,  ,
,  of a triangle
of a triangle  respectively. The circumcircles of triangles
respectively. The circumcircles of triangles 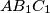 ,
, 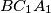 ,
, 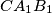 intersect the circumcircle of triangle
intersect the circumcircle of triangle  again at points
again at points 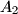 ,
, 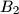 ,
, 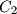 respectively (
respectively (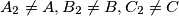 ). Points
). Points 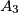 ,
, 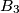 ,
, 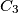 are symmetric to
are symmetric to 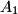 ,
, 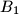 ,
, 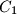 with respect to the midpoints of the sides
with respect to the midpoints of the sides  ,
,  ,
,  respectively. Prove that the triangles
respectively. Prove that the triangles 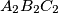 and
and 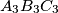 are similar.
are similar.
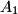 ,
, 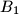 ,
, 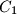 are chosen on the sides
are chosen on the sides  ,
,  ,
,  of a triangle
of a triangle  respectively. The circumcircles of triangles
respectively. The circumcircles of triangles 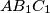 ,
, 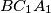 ,
, 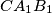 intersect the circumcircle of triangle
intersect the circumcircle of triangle  again at points
again at points 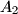 ,
, 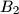 ,
, 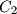 respectively (
respectively (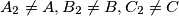 ). Points
). Points 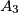 ,
, 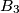 ,
, 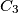 are symmetric to
are symmetric to 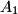 ,
, 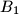 ,
, 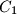 with respect to the midpoints of the sides
with respect to the midpoints of the sides  ,
,  ,
,  respectively. Prove that the triangles
respectively. Prove that the triangles 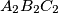 and
and 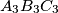 are similar.
are similar. Point  lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 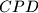 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 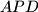 and
and 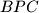 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 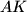 and
and 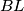 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear.
Author: Waldemar Pompe, Poland
 lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 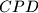 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 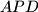 and
and 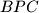 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 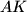 and
and 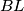 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear. Author: Waldemar Pompe, Poland
 Školjka
Školjka  be a variable point on the line
be a variable point on the line 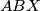 and
and 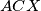 intersect at two distinct points
intersect at two distinct points 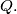 Prove that the line
Prove that the line  passes through a point independent of
passes through a point independent of  be the midpoint of the side
be the midpoint of the side  , and let
, and let  be a point on the circumcircle of triangle
be a point on the circumcircle of triangle 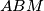 . Assume that the point
. Assume that the point 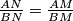 . Prove that the points
. Prove that the points 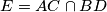 and
and 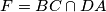 .
. 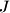 be the center of the excircle tangent to side
be the center of the excircle tangent to side 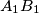 and
and  . Let
. Let 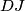 . Determine the angles
. Determine the angles 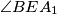 and
and 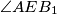 .
.