U trokutu

kutovi
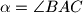
i
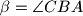
su šiljasti. S vanjske strane trokuta nad stranicama

i

, kao bazama, konstruirani su jednakokoračni trokuti

i
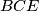
s vršnim kutovima
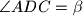
, odnosno
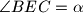
. Neka je

središte kružnice opisane trokutu

. Dokažite da je
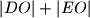
jednako opsegu trokuta

ako i samo ako je
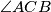
pravi.
%V0
U trokutu $ABC$ kutovi $\alpha=\angle BAC$ i $\beta = \angle CBA$ su šiljasti. S vanjske strane trokuta nad stranicama $\overline{AC}$ i $\overline{BC}$, kao bazama, konstruirani su jednakokoračni trokuti $ACD$ i $BCE$ s vršnim kutovima $\angle ADC = \beta$, odnosno $\angle BEC = \alpha$. Neka je $O$ središte kružnice opisane trokutu $ABC$. Dokažite da je $|DO| + |EO|$ jednako opsegu trokuta $ABC$ ako i samo ako je $\angle ACB$ pravi.