baza piramide
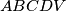
je pravokutnik

cije su duljine stranica
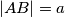
i
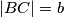
, a svi bocni bridovi su duljine

. odredite povrsinu presijeka te piramide ravninom koja prolazi dijagonalom

baze, i paralelna je bocnom bridu

.
%V0
baza piramide $ABCDV$ je pravokutnik $ABCD$ cije su duljine stranica $|AB| = a$ i $|BC| = b$, a svi bocni bridovi su duljine $c$. odredite povrsinu presijeka te piramide ravninom koja prolazi dijagonalom $\overline{BD}$ baze, i paralelna je bocnom bridu $\overline{VA}$.