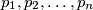
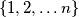
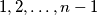
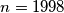
Pravci u ravnini su u općem položaju (nikoja dva nisu paralelna i nikoja tri se ne sijeku u istoj točki). Može li se svakom od sjecišta dvaju pravaca pridružiti jedan broj iz skupa tako da na svakom pravcu budu svi brojevi ako je a) , b) ?
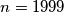
%V0
Pravci $p_1, p_2, \ldots, p_n$ u ravnini su u općem položaju (nikoja dva nisu paralelna i nikoja tri se ne sijeku u istoj točki). Može li se svakom od sjecišta dvaju pravaca pridružiti jedan broj iz skupa $\{1,2, \ldots n \}$ tako da na svakom pravcu budu svi brojevi $1,2, \ldots, n-1$ ako je
a) $n=1998$,
b) $n= 1999$?
Školjka 
u ravnini su u općem položaju (nikoja dva nisu paralelna i nikoja tri se ne sijeku u istoj točki). Može li se svakom od sjecišta dvaju pravaca pridružiti jedan broj iz skupa 
tako da na svakom pravcu budu svi brojevi 
ako je 
,
?