Mala olimpijada 1998 zadatak 2
Dodao/la:
mljulj12. travnja 2012. Neka su

i

sjecišta simetrala kutova

i
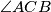
sa stranicama trokuta

i

trokuta

. Polupravac

siječe trokutu opisanu kružnicu u točki

. Dokažite da je
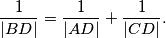
%V0
Neka su $M$ i $N$ sjecišta simetrala kutova $\angle ABC$ i $\angle ACB$ sa stranicama trokuta $\overline{AC}$ i $\overline{AB}$ trokuta $ABC$. Polupravac $MN$ siječe trokutu opisanu kružnicu u točki $D$. Dokažite da je
$$ \frac{1}{|BD|} = \frac{1}{|AD|}+ \frac{1}{|CD|} .$$
Izvor: Mala olimpijada 1998 zadatak 2