Neka je
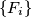
,
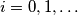
niz brojeva definiran na sljedeći način:
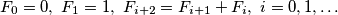
Za prirodan broj

neka su
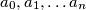
nenegativni brojevi koji zadovoljavaju uvjet
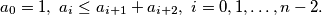
Dokažite da je
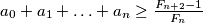
. Da li se postiže jednakost?
%V0
Neka je $\{ F_i \}$, $i=0,1, \ldots $ niz brojeva definiran na sljedeći način:
$$ F_0=0, \ F_1=1,\ F_{i+2}=F_{i+1}+F_{i}, \ i=0,1, \ldots$$
Za prirodan broj $n \geq 2$ neka su $a_0, a_1, \ldots a_n$ nenegativni brojevi koji zadovoljavaju uvjet
$$ a_0=1, \ a_i \leq a_{i+1} + a_{i+2}, \ i=0,1, \ldots, n-2. $$
Dokažite da je $a_0+a_1+\ldots+a_n \geq \frac{F_{n+2}-1}{F_{n}}$. Da li se postiže jednakost?