Mala olimpijada 1998 zadatak 6
Dodao/la:
mljulj12. travnja 2012. Neka je

skup svih nizova
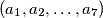
, pri čemu je
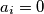
ili
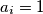
za svaki
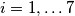
. Udaljenost

između dva elementa
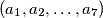
i
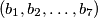
iz skupa

definiramo kao
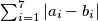
. Skup

je podksup skupa

takav da je udaljenost između svaka dva njegova elementa
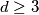
. Koliko najviše elemenata može imati skup

?
%V0
Neka je $S$ skup svih nizova $(a_1, a_2, \ldots, a_7)$, pri čemu je $a_i=0$ ili $a_i=1$ za svaki $i=1, \ldots 7$. Udaljenost $d$ između dva elementa $(a_1, a_2, \ldots, a_7)$ i $(b_1, b_2, \ldots, b_7)$ iz skupa $S$ definiramo kao $\sum_{i=1}^{7} {|a_i-b_i|}$. Skup $T$ je podksup skupa $S$ takav da je udaljenost između svaka dva njegova elementa $d \geq 3$. Koliko najviše elemenata može imati skup $T$?
Izvor: Mala olimpijada 1998 zadatak 6