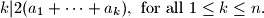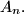Slični zadaci
A rectangular array of numbers is given. In each row and each column, the sum of all numbers is an integer. Prove that each nonintegral number  in the array can be changed into either
in the array can be changed into either  or
or 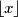 so that the row-sums and column-sums remain unchanged. (Note that
so that the row-sums and column-sums remain unchanged. (Note that  is the least integer greater than or equal to
is the least integer greater than or equal to  , while
, while 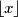 is the greatest integer less than or equal to
is the greatest integer less than or equal to  .)
.)
 in the array can be changed into either
in the array can be changed into either  or
or 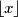 so that the row-sums and column-sums remain unchanged. (Note that
so that the row-sums and column-sums remain unchanged. (Note that  is the least integer greater than or equal to
is the least integer greater than or equal to  , while
, while 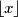 is the greatest integer less than or equal to
is the greatest integer less than or equal to  .)
.) Cards numbered 1 to 9 are arranged at random in a row. In a move, one may choose any block of consecutive cards whose numbers are in ascending or descending order, and switch the block around. For example, 9 1 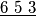
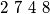 may be changed to
may be changed to 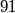
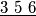
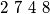 . Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
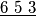
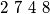 may be changed to
may be changed to 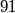
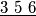
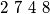 . Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order. Let 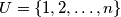 , where
, where 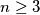 . A subset
. A subset  of
of  is said to be split by an arrangement of the elements of
is said to be split by an arrangement of the elements of  if an element not in
if an element not in  occurs in the arrangement somewhere between two elements of
occurs in the arrangement somewhere between two elements of  . For example, 13542 splits
. For example, 13542 splits 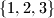 but not
but not 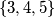 . Prove that for any
. Prove that for any  subsets of
subsets of  , each containing at least 2 and at most
, each containing at least 2 and at most 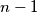 elements, there is an arrangement of the elements of
elements, there is an arrangement of the elements of  which splits all of them.
which splits all of them.
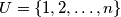 , where
, where 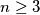 . A subset
. A subset  of
of  is said to be split by an arrangement of the elements of
is said to be split by an arrangement of the elements of  if an element not in
if an element not in  occurs in the arrangement somewhere between two elements of
occurs in the arrangement somewhere between two elements of  . For example, 13542 splits
. For example, 13542 splits 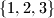 but not
but not 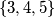 . Prove that for any
. Prove that for any  subsets of
subsets of  , each containing at least 2 and at most
, each containing at least 2 and at most 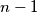 elements, there is an arrangement of the elements of
elements, there is an arrangement of the elements of  which splits all of them.
which splits all of them. This ISL 2005 problem has not been used in any TST I know. A pity, since it is a nice problem, but in its shortlist formulation, it is absolutely incomprehensible. Here is a mathematical restatement of the problem:
Let be a nonnegative integer.
be a nonnegative integer.
A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex is called an extended successor of a vertex
is called an extended successor of a vertex 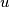 if there is a chain of vertices
if there is a chain of vertices 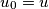 ,
, 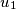 ,
, 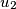 , ...,
, ..., 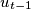 ,
, 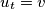 with
with 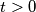 such that the vertex
such that the vertex 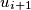 is a successor of the vertex
is a successor of the vertex 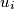 for every integer
for every integer  with
with 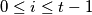 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.
Prove that if the forest has vertices, then there are at most
vertices, then there are at most 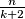 dynastic vertices.
dynastic vertices.
Let
 be a nonnegative integer.
be a nonnegative integer.A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex
 is called an extended successor of a vertex
is called an extended successor of a vertex 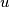 if there is a chain of vertices
if there is a chain of vertices 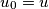 ,
, 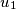 ,
, 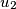 , ...,
, ..., 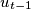 ,
, 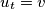 with
with 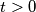 such that the vertex
such that the vertex 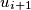 is a successor of the vertex
is a successor of the vertex 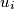 for every integer
for every integer  with
with 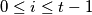 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.Prove that if the forest has
 vertices, then there are at most
vertices, then there are at most 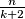 dynastic vertices.
dynastic vertices. Consider 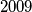 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 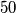 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
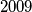 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 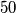 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
 Školjka
Školjka 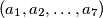 , pri čemu je
, pri čemu je 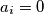 ili
ili 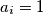 za svaki
za svaki 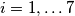 . Udaljenost
. Udaljenost  između dva elementa
između dva elementa 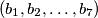 iz skupa
iz skupa 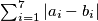 . Skup
. Skup  je podksup skupa
je podksup skupa 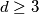 . Koliko najviše elemenata može imati skup
. Koliko najviše elemenata može imati skup 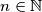 and
and 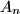 set of all permutations
set of all permutations  of the set
of the set 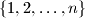 for which
for which