Zadan je jednakostraničan trokut. Dozvoljeni potez je da pravcem presiječemo trenutni lik na dva dijela, "okrenemo" jedan od nastalih dijelova i ponovo ”zalijepimo”. (npr. ako to napravimo po visini jednakostraničnog trokuta stranice  , dobit ćemo paralelogram stranica
, dobit ćemo paralelogram stranica 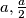 i kutom od
i kutom od 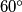 ) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži!
) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži!
 , dobit ćemo paralelogram stranica
, dobit ćemo paralelogram stranica 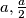 i kutom od
i kutom od 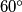 ) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži!
) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži! Slični zadaci
U Sunčevom sustavu otkriven je novi planet! Dakle, oko Sunca kruži  planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše
planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše  planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.)
planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.)
 planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše
planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše  planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.)
planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.)  Školjka
Školjka 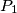 ,
, 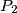 ,
, 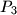 ,
, 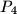 ,
, 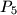 sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par
sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par 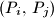 za
za 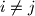 tako da pravac
tako da pravac 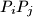 sadrži neku točku
sadrži neku točku  sa cjelobrojnim koordinatama koja leži između
sa cjelobrojnim koordinatama koja leži između 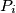 i
i 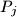 .
.  i
i  , dok je
, dok je  varijabilna, takva da je
varijabilna, takva da je  fiksan. Polovišta stranica
fiksan. Polovišta stranica  i
i  su točke
su točke  i
i  redom. Točke
redom. Točke  i
i  su takve da je
su takve da je 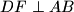 i
i 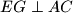 , a
, a 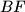 i
i 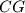 su okomite na
su okomite na  . Dokažite da umnožak
. Dokažite da umnožak  ne ovisi o položaju točke
ne ovisi o položaju točke  povučene su simetrale
povučene su simetrale  i
i  kutova
kutova 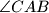 i
i  (
( i
i 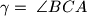 ako je
ako je 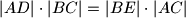 i
i 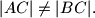
 iz unutrašnjosti ili s ruba trokuta
iz unutrašnjosti ili s ruba trokuta 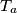 ,
, 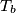 ,
, 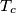 su redom nožišta okomica iz
su redom nožišta okomica iz  ,
, 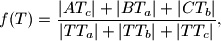 dokažite da
dokažite da 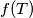 ne ovisi o izboru točke
ne ovisi o izboru točke  dano je
dano je  zelenih i
zelenih i  koji sadrži
koji sadrži