MEMO 2007 pojedinačno problem 3
Dodao/la:
arhiva28. travnja 2012. Let

be a circle and
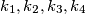
four smaller circles with their centres
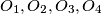
respectively, on

. For
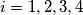
and
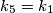
the circles
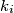
and
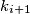
meet at
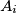
and
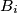
such that
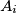
lies on

. The points
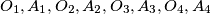
lie in that order on

and are pairwise different.
Prove that
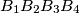
is a rectangle.
%V0
Let $k$ be a circle and $k_{1},k_{2},k_{3},k_{4}$ four smaller circles with their centres $O_{1},O_{2},O_{3},O_{4}$ respectively, on $k$. For $i = 1,2,3,4$ and $k_5=k_1$ the circles $k_i$ and $k_{i+1}$ meet at $A_i$ and $B_i$ such that $A_i$ lies on $k$. The points $O_{1},A_{1},O_{2},A_{2},O_{3},A_{3},O_{4},A_{4}$ lie in that order on $k$ and are pairwise different.
Prove that $B_{1}B_{2}B_{3}B_{4}$ is a rectangle.
Izvor: Srednjoeuropska matematička olimpijada 2007, pojedinačno natjecanje, problem 3