MEMO 2007 ekipno problem 5
Dodao/la:
arhiva28. travnja 2012. Let
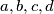
be real numbers which satisfy
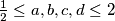
and
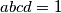
. Find the maximum value of
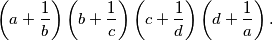
%V0
Let $a,b,c,d$ be real numbers which satisfy $\frac{1}{2}\leq a,b,c,d\leq 2$ and $abcd=1$. Find the maximum value of $$\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)\left(c+\frac{1}{d}\right)\left(d+\frac{1}{a}\right)\text{.}$$
Izvor: Srednjoeuropska matematička olimpijada 2007, ekipno natjecanje, problem 5