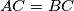
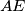
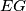
Let be an isosceles triangle with . Its incircle touches in and in . A line distinct of goes through and intersects the incircle in and . Line intersects line and in and , respectively. Prove that .
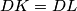
%V0
Let $ABC$ be an isosceles triangle with $AC = BC$. Its incircle touches $AB$ in $D$ and $BC$ in $E$. A line distinct of $AE$ goes through $A$ and intersects the incircle in $F$ and $G$. Line $AB$ intersects line $EF$ and $EG$ in $K$ and $L$, respectively. Prove that $DK = DL$.
Izvor: Srednjoeuropska matematička olimpijada 2008, pojedinačno natjecanje, problem 3
Školjka 
be an isosceles triangle with 
. Its incircle touches 
in 
and 
in 
. A line distinct of 
goes through 
and intersects the incircle in 
and 
. Line 
and 
in 
and 
, respectively. Prove that 
.