MEMO 2008 ekipno problem 8
Dodao/la:
arhiva28. travnja 2012. Prove: If the sum of all positive divisors of
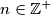
is a power of two, then the number/amount of the divisors is a power of two.
%V0
Prove: If the sum of all positive divisors of $n \in \mathbb{Z}^{+}$ is a power of two, then the number/amount of the divisors is a power of two.
Izvor: Srednjoeuropska matematička olimpijada 2008, ekipno natjecanje, problem 8