MEMO 2009 pojedinačno problem 1
Dodao/la:
arhiva28. travnja 2012. Find all functions
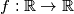
, such that
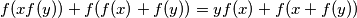
holds for all

,
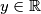
, where
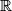
denotes the set of real numbers.
%V0
Find all functions $f: \mathbb{R} \to \mathbb{R}$, such that $$f(xf(y)) + f(f(x) + f(y)) = yf(x) + f(x + f(y))$$ holds for all $x$, $y \in \mathbb{R}$, where $\mathbb{R}$ denotes the set of real numbers.
Izvor: Srednjoeuropska matematička olimpijada 2009, pojedinačno natjecanje, problem 1