MEMO 2009 pojedinačno problem 2
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,0 Suppose that we have 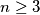 distinct colours. Let
distinct colours. Let  be the greatest integer with the property that every side and every diagonal of a convex polygon with
be the greatest integer with the property that every side and every diagonal of a convex polygon with  vertices can be coloured with one of
vertices can be coloured with one of  colours in the following way:
colours in the following way:
(i) At least two colours are used,
(ii) any three vertices of the polygon determine either three segments of the same colour or of three different colours.
Show that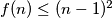 with equality for infintely many values of
with equality for infintely many values of  .
.
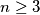 distinct colours. Let
distinct colours. Let  be the greatest integer with the property that every side and every diagonal of a convex polygon with
be the greatest integer with the property that every side and every diagonal of a convex polygon with  vertices can be coloured with one of
vertices can be coloured with one of  colours in the following way:
colours in the following way: (i) At least two colours are used,
(ii) any three vertices of the polygon determine either three segments of the same colour or of three different colours.
Show that
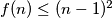 with equality for infintely many values of
with equality for infintely many values of  .
. Izvor: Srednjoeuropska matematička olimpijada 2009, pojedinačno natjecanje, problem 2
 Školjka
Školjka 
