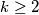
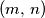
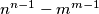
Determine all integers such that for all pairs of different positive integers not greater than , the number is not divisible by .
%V0
Determine all integers $k\ge 2$ such that for all pairs $(m,\,n)$ of different positive integers not greater than $k$, the number $n^{n-1}-m^{m-1}$ is not divisible by $k$.
Izvor: Srednjoeuropska matematička olimpijada 2009, pojedinačno natjecanje, problem 4
Školjka 
such that for all pairs 
of different positive integers not greater than 
, the number 
is not divisible by