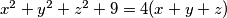
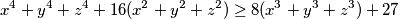
Let , , be real numbers satisfying . Prove that and determine when equality holds.
%V0
Let $x$, $y$, $z$ be real numbers satisfying $x^2+y^2+z^2+9=4(x+y+z)$. Prove that $$x^4+y^4+z^4+16(x^2+y^2+z^2) \ge 8(x^3+y^3+z^3)+27$$ and determine when equality holds.
Izvor: Srednjoeuropska matematička olimpijada 2009, ekipno natjecanje, problem 1
Školjka 
, 
, 
be real numbers satisfying 
. Prove that 
and determine when equality holds.