MEMO 2009 ekipno problem 4
Kvaliteta:
Avg: 2,0Težina:
Avg: 3,5 We colour every square of the 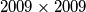 board with one of
board with one of  colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum
colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum  , such that for every colouring of the board at least on colour present at the board is connected.
, such that for every colouring of the board at least on colour present at the board is connected.
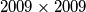 board with one of
board with one of  colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum
colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum  , such that for every colouring of the board at least on colour present at the board is connected.
, such that for every colouring of the board at least on colour present at the board is connected. Izvor: Srednjoeuropska matematička olimpijada 2009, ekipno natjecanje, problem 4
 Školjka
Školjka 
