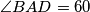
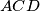
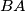
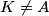
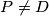
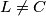
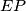
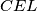
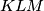
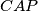
Let be a parallelogram with and denote by the intersection of its diagonals. The circumcircle of triangle meets the line at , the line at and the line at . The line intersects the circumcircle of triangle at points and . Prove that triangles and are congruent.
%V0
Let $ABCD$ be a parallelogram with $\angle BAD = 60$ and denote by $E$ the intersection of its diagonals. The circumcircle of triangle $ACD$ meets the line $BA$ at $K \ne A$, the line $BD$ at $P \ne D$ and the line $BC$ at $L\ne C$. The line $EP$ intersects the circumcircle of triangle $CEL$ at points $E$ and $M$. Prove that triangles $KLM$ and $CAP$ are congruent.
Izvor: Srednjoeuropska matematička olimpijada 2009, ekipno natjecanje, problem 5
Školjka 
be a parallelogram with 
and denote by 
the intersection of its diagonals. The circumcircle of triangle 
meets the line 
at 
, the line 
at 
and the line 
at 
. The line 
intersects the circumcircle of triangle 
at points 
. Prove that triangles 
and 
are congruent.