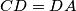
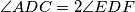
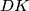
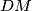
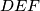
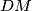
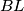
Suppose that is a cyclic quadrilateral and . Points and belong to the segments and respectively, and . Segments and are height and median of triangle , respectively. is the point symmetric to with respect to . Prove that the lines and are parallel.
%V0
Suppose that $ABCD$ is a cyclic quadrilateral and $CD=DA$. Points $E$ and $F$ belong to the segments $AB$ and $BC$ respectively, and $\angle ADC=2\angle EDF$. Segments $DK$ and $DM$ are height and median of triangle $DEF$, respectively. $L$ is the point symmetric to $K$ with respect to $M$. Prove that the lines $DM$ and $BL$ are parallel.
Izvor: Srednjoeuropska matematička olimpijada 2009, ekipno natjecanje, problem 6
Školjka 
is a cyclic quadrilateral and 
. Points 
and 
belong to the segments 
and 
respectively, and 
. Segments 
and 
are height and median of triangle 
, respectively. 
is the point symmetric to 
with respect to 
. Prove that the lines 
are parallel.