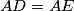
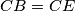
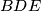
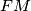
We are given a cyclic quadrilateral with a point on the diagonal such that and . Let be the center of the circumcircle of the triangle . The circle intersects the line in the points and . Prove that the lines , and meet at one point.
%V0
We are given a cyclic quadrilateral $ABCD$ with a point $E$ on the diagonal $AC$ such that $AD=AE$ and $CB=CE$. Let $M$ be the center of the circumcircle $k$ of the triangle $BDE$. The circle $k$ intersects the line $AC$ in the points $E$ and $F$. Prove that the lines $FM$, $AD$ and $BC$ meet at one point.
Izvor: Srednjoeuropska matematička olimpijada 2010, pojedinačno natjecanje, problem 3
Školjka 
with a point 
on the diagonal 
such that 
and 
. Let 
be the center of the circumcircle 
of the triangle 
. The circle 
. Prove that the lines 
, 
and 
meet at one point.