MEMO 2010 pojedinačno problem 4
Dodao/la:
arhiva28. travnja 2012. Find all positive integers

which satisfy the following tow conditions:
(a)

has at least four different positive divisors;
(b) for any divisors

and

of

satisfying
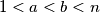
, the number
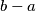
divides

.
%V0
Find all positive integers $n$ which satisfy the following tow conditions:
(a) $n$ has at least four different positive divisors;
(b) for any divisors $a$ and $b$ of $n$ satisfying $1<a<b<n$, the number $b-a$ divides $n$.
Izvor: Srednjoeuropska matematička olimpijada 2010, pojedinačno natjecanje, problem 4