MEMO 2010 ekipno problem 1
Dodao/la:
arhiva28. travnja 2012. Three strictly increasing sequences
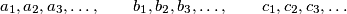
of positive integers are given. Every positive integer belongs to exactly one of the three sequences. For every positive integer

, the following conditions hold:
(a)
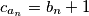
;
(b)
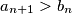
;
(c) the number
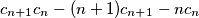
is even.
Find
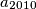
,
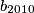
and
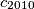
.
%V0
Three strictly increasing sequences
$$a_1, a_2, a_3, \ldots,\qquad b_1, b_2, b_3, \ldots,\qquad c_1, c_2, c_3, \ldots$$
of positive integers are given. Every positive integer belongs to exactly one of the three sequences. For every positive integer $n$, the following conditions hold:
(a) $c_{a_n}=b_n+1$;
(b) $a_{n+1}>b_n$;
(c) the number $c_{n+1}c_{n}-(n+1)c_{n+1}-nc_n$ is even.
Find $a_{2010}$, $b_{2010}$ and $c_{2010}$.
Izvor: Srednjoeuropska matematička olimpijada 2010, ekipno natjecanje, problem 1