MEMO 2010 ekipno problem 2
Dodao/la:
arhiva28. travnja 2012. For each integer
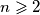
, determine the largest real constant
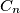
such that for all positive real numbers
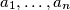
we have
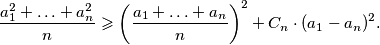
%V0
For each integer $n\geqslant2$, determine the largest real constant $C_n$ such that for all positive real numbers $a_1, \ldots, a_n$ we have $$\frac{a_1^2+\ldots+a_n^2}{n}\geqslant\left(\frac{a_1+\ldots+a_n}{n}\right)^2+C_n\cdot(a_1-a_n)^2\mbox{.}$$
Izvor: Srednjoeuropska matematička olimpijada 2010, ekipno natjecanje, problem 2