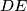
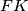
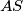
The incircle of the triangle touches the sides , , and in the points , and , respectively. Let be the point symmetric to with respect to the incenter. The lines and intersect at . Prove that is parallel to .
%V0
The incircle of the triangle $ABC$ touches the sides $BC$, $CA$, and $AB$ in the points $D$, $E$ and $F$, respectively. Let $K$ be the point symmetric to $D$ with respect to the incenter. The lines $DE$ and $FK$ intersect at $S$. Prove that $AS$ is parallel to $BC$.
Izvor: Srednjoeuropska matematička olimpijada 2010, ekipno natjecanje, problem 5
Školjka 
touches the sides 
, 
, and 
in the points 
, 
and 
, respectively. Let 
be the point symmetric to 
and 
intersect at 
. Prove that 
is parallel to