MEMO 2010 ekipno problem 6
Dodao/la:
arhiva28. travnja 2012. Let

,

,

,

,

be points such that

is a cyclic quadrilateral and
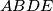
is a parallelogram. The diagonals

and
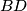
intersect at

and the rays

and
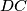
intersect at

. Prove that
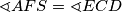
.
%V0
Let $A$, $B$, $C$, $D$, $E$ be points such that $ABCD$ is a cyclic quadrilateral and $ABDE$ is a parallelogram. The diagonals $AC$ and $BD$ intersect at $S$ and the rays $AB$ and $DC$ intersect at $F$. Prove that $\sphericalangle{AFS}=\sphericalangle{ECD}$.
Izvor: Srednjoeuropska matematička olimpijada 2010, ekipno natjecanje, problem 6