MEMO 2011 ekipno problem 3
Dodao/la:
arhivaApril 28, 2012 For an integer
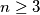
, let
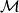
be the set
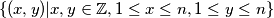
of points in the plane.
What is the maximum possible number of points in a subset
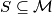
which does not contain three distinct points being the vertices of a right triangle?
%V0
For an integer $n \geq 3$, let $\mathcal M$ be the set $\{(x, y) | x, y \in \mathbb Z, 1 \leq x \leq n, 1 \leq y \leq n\}$ of points in the plane.
What is the maximum possible number of points in a subset $S \subseteq \mathcal M$ which does not contain three distinct points being the vertices of a right triangle?
Source: Srednjoeuropska matematička olimpijada 2011, ekipno natjecanje, problem 3
Školjka 
