MEMO 2011 ekipno problem 6
Kvaliteta:
Avg: 2,0Težina:
Avg: 6,0 Let  be an acute triangle. Denote by
be an acute triangle. Denote by 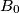 and
and 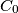 the feet of the altitudes from vertices
the feet of the altitudes from vertices  and
and  , respectively. Let
, respectively. Let  be a point inside the triangle
be a point inside the triangle  such that the line
such that the line 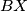 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 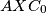 and the line
and the line 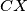 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 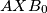 . Show that the line
. Show that the line 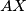 is perpendicular to
is perpendicular to  .
.
 be an acute triangle. Denote by
be an acute triangle. Denote by 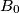 and
and 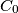 the feet of the altitudes from vertices
the feet of the altitudes from vertices  and
and  , respectively. Let
, respectively. Let  be a point inside the triangle
be a point inside the triangle  such that the line
such that the line 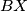 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 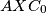 and the line
and the line 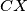 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 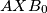 . Show that the line
. Show that the line 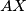 is perpendicular to
is perpendicular to  .
. Izvor: Srednjoeuropska matematička olimpijada 2011, ekipno natjecanje, problem 6
 Školjka
Školjka 
